Contoh Soal Pergeseran Grafik Fungsi Kuadrat
Contoh Soal Pergeseran Grafik Fungsi Kuadrat - Sebagai ilustrasi, yuk kita cermati grafik fungsi berikut.
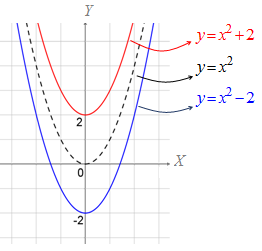
Berdasarkan ilustrasi di atas, dapat kita simpulkan bahwa grafik fungsi diperoleh dengan cara menggeser grafik fungsi sejauh satuan searah sumbu . Jika , maka pergeseran ke arah atas, sebaliknya jika , maka pergeseran ke arah bawah.


Jika kita cermati dengan seksama, tampak bahwa
- grafik fungsi diperoleh dengan cara menggeser grafik fungsi ke atas sejauh dua satuan, sehingga titik puncaknya adalah
- grafik fungsi diperoleh dengan cara menggeser grafik fungsi ke bawah sejauh dua satuan, sehingga titik puncaknya adalah
Berdasarkan ilustrasi di atas, dapat kita simpulkan bahwa grafik fungsi diperoleh dengan cara menggeser grafik fungsi sejauh satuan searah sumbu . Jika , maka pergeseran ke arah atas, sebaliknya jika , maka pergeseran ke arah bawah.
Konsep Dasar II

Apa yang dapat kalian simpulkan dari ketiga grafik fungsi di atas?
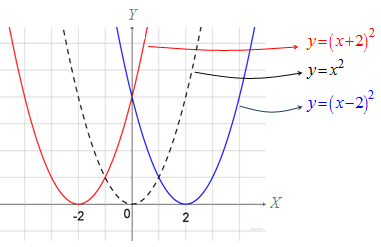
Jika kita cermati dengan seksama, tampak bahwa
- grafik fungsi diperoleh dengan cara menggeser grafik fungsi ke kiri sejauh dua satuan, sehingga titik puncaknya adalah
- grafik fungsi diperoleh dengan cara menggeser grafik fungsi ke kanan sejauh dua satuan, sehingga titik puncaknya adalah
Jadi, secara umum dapat kita simpulkan bahwa grafik fungsi diperoleh dengan cara menggeser grafik fungsi sejauh satuan searah sumbu . Jika , maka pergeseran ke arah kiri, sebaliknya jika , maka pergerseran ke arah kanan.
Konsep Dasar III
Pada konsep dasar III ini, kita akan mencari tahu hubungan antara grafik fungsi dengan grafik fungsi .
Nah, sebagai ilustrasi, yuk kita cermati grafik fungsi berikut.

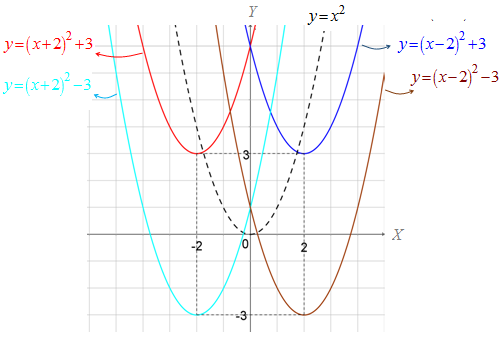
Pada gambar di atas, tampak bahwa:
- grafik fungsi diperoleh dengan cara menggeser grafik fungsi ke atas sejauh tiga satuan, kemudian menggesernya ke kiri sebesar dua satuan
- grafik fungsi diperoleh dengan cara menggeser grafik fungsi ke atas sejauh tiga satuan, kemudian menggesernya ke kanan sebesar dua satuan
- grafik fungsi diperoleh dengan cara menggeser grafik fungsi ke bawah sejauh tiga satuan, kemudian menggesernya ke kiri sebesar dua satuan
- grafik fungsi diperoleh dengan cara menggeser grafik fungsi ke atas sejauh tiga satuan, kemudian menggesernya ke kanan sebesar dua satuan
Jadi, dapat kita simpulkan bahwa grafik fungsi diperoleh dengan menggeser grafik fungsi searah sumbu sejauh satuan, kemudian menggesernya searah sumbu sejauh satuan. Jika , maka arah pergeseran adalah ke atas dan jika , maka arah pergeseran adalah ke kiri.

S1
Grafik fungsi diperoleh dengan cara menggeser grafik fungsi sejauh ….
S2
Grafik fungsi diperoleh dengan cara menggeser grafik fungsi sejauh ….
S3
Grafik fungsi diperoleh dengan cara menggeser grafik fungsi sejauh ….
S4
Titik puncak dari grafik fungsi adalah ….
S5

Grafik fungsi adalah ….
S6
Grafik fungsi adalah ….
S7
Sebuah grafik fungsi kuadrat diperoleh dengan cara menggeser grafik fungsi sejauh 4 satuan ke kiri dan 7 satuan ke bawah. Grafik fungsi kuadrat tersebut adalah ….
S8
Sebuah grafik fungsi kuadrat diperoleh dengan cara menggeser grafik fungsi sejauh 3 satuan ke kanan dan 5 satuan ke atas. Grafik fungsi kuadrat tersebut adalah ….
S9
Grafik fungsi adalah ….
S10
Grafik fungsi adalah ….
Tags:
matematika


