Contoh Soal Sumbu Simetri dan Nilai Optimum Fungsi Kuadrat
Contoh Soal Sumbu Simetri dan Nilai Optimum Fungsi Kuadrat - Pada topik sebelumnya kalian telah belajar tentang fungsi kuadrat dan grafik fungsi kuadrat. Nah, pada topik kali ini kalian akan belajar menentukan persamaan sumbu simetri dan nilai optimum fungsi kuadrat
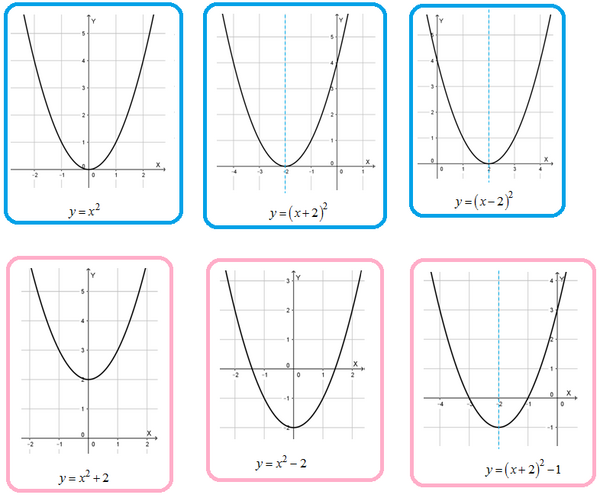

Nah, apa yang dapat kamu simpulkan dari tabel di atas?
Yuk kita cermati uraian berikut.
Apakah kalian masih ingat pengaruh nilai terhadap titik optimum?
Apakah kalian sudah paham dengan penjelasan di atas?
Penyelesaian:
Dari fungsi kuadrat kita ketahui bahwa , , dan .
Penyelesaian:
Dari fungsi kuadrat kita ketahui bahwa , , dan .
dengan memperhatikan nilai , , dan .
Konsep Dasar

Tahukah kalian persamaan sumbu simetri dan nilai optimum dari keenam grafik fungsi kuadrat di atas?
Jika kalian cermati dengan seksama, maka kalian akan mendapatkan hasil sebagai berikut:

Nah, apa yang dapat kamu simpulkan dari tabel di atas?
Ya, ternyata jika titik puncak suatu grafik fungsi kuadrat adalah , maka adalah persamaan sumbu simetri, sedangkan adalah nilai optimum.
Yuk kita cermati uraian berikut.
Berdasarkan konsep pergeseran grafik fungsi, dapat kita simpulkan bahwa koordinat titik puncak dari grafik fungsi adalah , dengan dan , dimana .
Dengan demikian, dapat kita simpulkan bahwa persamaan sumbu simetri dari grafik fungsi adalah , sedangkan nilai optimumnya adalah .
Apakah kalian masih ingat pengaruh nilai terhadap titik optimum?
Seperti yang telah kalian pelajari pada topik sebelumnya, kita ketahui bahwa:
- Jika , maka kurva akan membuka ke bawah, sehingga titik puncak kurva merupakan titik balik maksimum.
- Jika , maka kurva akan membuka ke atas, sehingga titik puncak kurva merupakan titik balik minimum.
Apakah kalian sudah paham dengan penjelasan di atas?
Yuk kita cermati beberapa contoh soal berikut agar kalian semakin paham.
Contoh 1
Tentukan persamaan sumbu simetri dan nilai optimum dari fungsi kuadrat .
Penyelesaian:
Dari fungsi kuadrat kita ketahui bahwa , , dan .
Persamaan sumbu simetri dari grafik fungsi kuadrat adalah .
Dengan demikian, nilai optimum dari grafik fungsi kuadrat adalah .
Nah, jika kita gunakan rumus, nilai optimum yang diperoleh juga sama, yaitu
Contoh 2
Jika nilai minimum dari fungsi kuadrat adalah , maka berapakah nilai yang memenuhi?
Penyelesaian:
Dari fungsi kuadrat kita ketahui bahwa , , dan .
Jika kita gunakan rumus nilai optimum, maka akan kita peroleh hasil sebagai berikut:
Berdasarkan uraian di atas, dapat kita simpulkan bahwa .
S1
Persamaan sumbu simetri grafik fungsi kuadrat adalah ….
S2
Jika persamaan sumbu simetri dari grafik fungsi kuadrat adalah , maka nilai adalah ….
S3
Nilai optimum fungsi kuadrat adalah ….
S4
Jika nilai optimum dari fungsi kuadrat adalah , maka nilai adalah ….
S5
Titik balik minimum dari grafik fungsi kuadrat adalah ….
S6
Titik balik minimum dari grafik fungsi kuadrat adalah ….
S7
Jika titik puncak grafik fungsi kuadrat adalah , maka nilai dari adalah ….
S8
Diketahui persamaan sumbu simetri dari grafik fungsi kuadrat adalah . Nilai optimumnya adalah ….
S9
Diketahui bahwa nilai minimum dari fungsi kuadrat adalah tiga. Nilai adalah ….
S10
Diketahui nilai minimum grafik fungsi kuadrat adalah . Jika , maka persamaan sumbu simetrinya adalah ….
Tags:
matematika


