Beranda

Contoh Soal Menentukan Persamaan Kurva

Jeger
Jeger
Posting Komentar
komentar teratas
Terbaru dulu
Contoh Soal Menentukan Persamaan Kurva - Misalkan turunan suatu fungsi F (x) adalah F ‘ (x) = f (x). Fungsi asal F (x) dapat ditentukan melalui proses pengintegralan sesuai definisi integral tak tentu.
∫F′(x)dx=F(x)+C
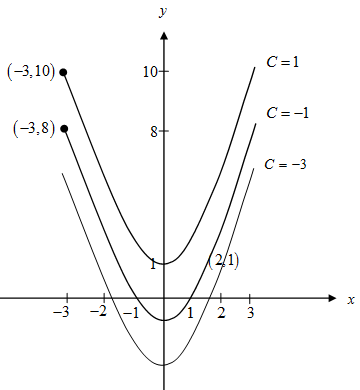
Dalam hal ini, nilai konstanta C dapat ditentukan jika diketahui nilai tertentu dari variabel x dan F (x) dari ∫F′(x)dx. Nilai C diperoleh dengan cara mensubstitusikan kedua nilai variabel yang bersesuaian ke dalam hasil pengintegralan. Ini berarti, terdapat tak berhingga banyaknya fungsi yang memiliki diferensial F ‘ (x). Setiap fungsi tersebut hanya berbeda pada nilai C. Perhatikan gambar kurva di bawah ini dengan beberapa nilai C yang memenuhi suatu persamaan diferensial.
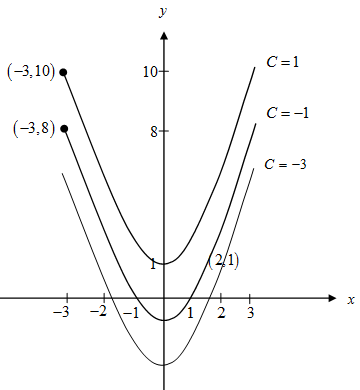
Misalkan dydx=2x adalah gradien garis singgung kurva y = F (x) pada setiap titik (x, y). Dengan menggunakan notasi kalkulus diferensial untuk gradien diperoleh:
dydx=2x
⇔dy=2xdx
⇔∫dy=∫2xdx
⇔y=x2+C, untuk setiap C Ïµ ÉŒ ... (1)
Kurva y = x2 + C yang ditunjukkan pada gambar di atas memiliki gradien garis singgung yang sama untuk nilai x yang sama. Dengan mengamati kembali gambar tersebut, tampak bahwa kurva y = x2 + C merupakan himpunan kurva berbentuk parabola dalam interval -3 ≤ x ≤ 3. Jika kurva itu melalui titik (-3, 10), maka dengan mensubstitusikan titik yang dilalui ke persamaan (1) diperoleh nilai C sebagai berikut.
y=x2+C
⇔10=(−3)2+C
⇔10=9+C
⇔C=1
Ini berarti, persamaan kurvanya adalah y = x2 + 1.
Jika kurva (parabola) tersebut melalui titik (-3, 8), maka:
y=x2+C
⇔8=(−3)2+C
⇔8=9+C
⇔C=−1
Ini berarti, persamaan kurvanya nya adalah y = x2 – 1.
Jika kurva (parabola) tersebut melalui titik (2, 1), maka:
y=x2+C
⇔1=(2)2+C
⇔1=4+C
⇔C=−3
Ini berarti, persamaan parabolanya adalah y = x2 – 3.
Contoh Soal Menentukan Persamaan Kurva

SOAL 1
Sebuah kurva y = f (x) melalui titik A (2, 0). Jika gradien garis singgung di titik A adalah dydx=2x–4, maka persamaan kurva tersebut adalah ….

SOAL 2
Suatu kurva melalui titik P (1, 3). Gradien garis singgung kurva tersebut di titik T (x, y) sama dengan dydx=2x−5. Persamaan kurva tersebut adalah ….

SOAL 3
Suatu kurva melalui titik B (2, 8). Gradien garis singgung kurva tersebut di titik P (x, y) sama dengan dydx=2x–1. Persamaan kurva yang memenuhi adalah ….

SOAL 4
Diketahui f ‘ (x) = 6x2 + 4. Persamaan f (x) yang melalui titik (1, 1) adalah ....

SOAL 5
Persamaan kurva yang melalui titik (2, 4) dengan gradien garis singgungnya dydx=6x2−4x+1adalah ….

SOAL 6
Persamaan kurva yang melalui titik (1, -3) dengan persamaan gradien garis singgung dydx=6x2−4x+3 adalah ….

SOAL 7
Gradien garis singgung kurva y = f (x) dinyatakan dengan dydx=3x(2−x). Persamaan kurva yang melalui titik (-1, 10) adalah …

SOAL 8
Gradien garis singgung suatu kurva di titik (x, y) adalah 3x. Jika kurva ini melalui titik (4, 9), maka persamaan garis singgung kurva ini di titik berabsis 1 adalah ….

SOAL 9
Diketahui gradien garis singgung kurva y = f (x) di titik (a, b) adalah 2a3+6a2+6a+4. Jika kurva melalui titik (−1,−112), maka persamaan kurva tersebut adalah ….

SOAL 10
Diketahui dydx berbanding terbalik dengan x2.
Jika saat x = 2 diperoleh dydx=5 dan y = 1, maka nilai y pada saat x = -2 adalah ….
Jeger
Jeger
Suka Berbagi, Suka Belajar, Juga Suka Kamu, Iya Kamu!
Tags:
Matematika Ipa kelas 12
Link copied to clipboard.