Contoh Soal Menggambar Grafik Fungsi y = ax^2 dan y = ax^2 + c
Contoh Soal Menggambar Grafik Fungsi y = ax^2 dan y = ax^2 + c - Pada topik sebelumnya kalian telah belajar mengenai pengertian fungsi kuadrat. Nah, pada topik kali ini kalian akan belajar menggambar grafik fungsi kuadrat berbentuk
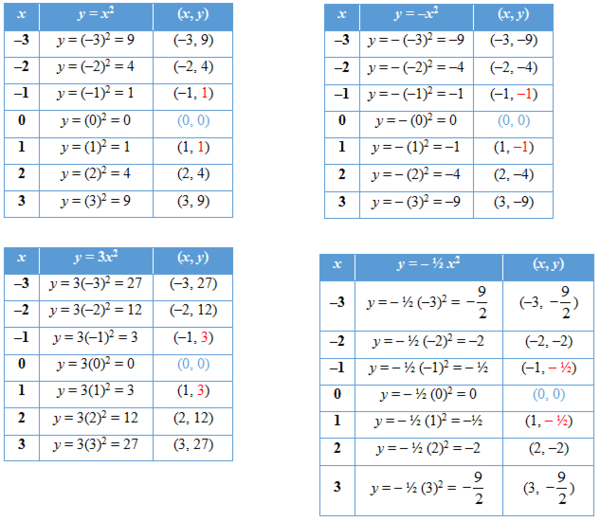
Apa yang dapat kalian simpulkan dari grafik fungsi kuadrat di atas?
Lalu bagaimanakah sifat grafik fungsi kuadrat berbentuk , dengan dan ?
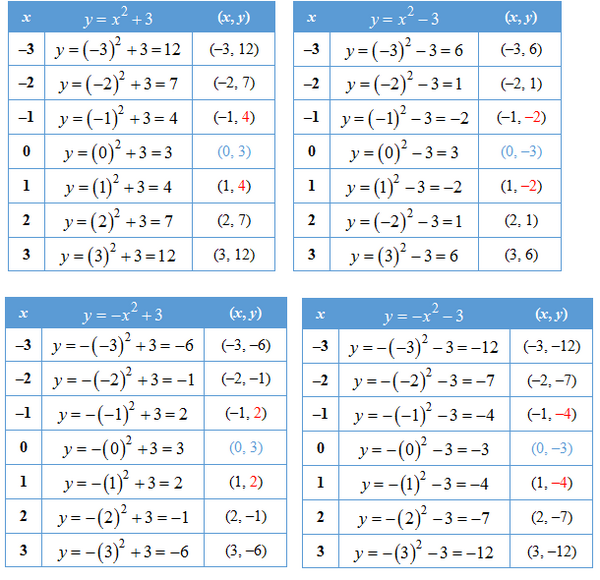
Coba tebak, apa saja sifat dari grafik fungsi kuadrat berbentuk ?

dan , dengan dan .
Konsep Dasar
Tahukah kalian bagaimana cara menggambar kedua grafik tersebut?
Ada dua langkah yang perlu kalian ikuti untuk menggambar grafik fungsi kuadrat, yaitu:
- Membuat tabel nilai fungsi untuk menentukan titik-titik yang dilalui grafik fungsi kuadrat.
- Menghubungkan semua titik yang diperoleh dalam koordinat Kartesius.
Grafik Fungsi y = ax2
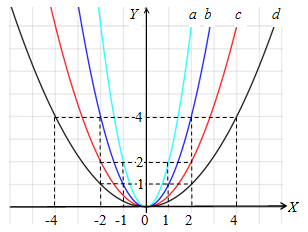
Sebagai ilustrasi, kita akan mencoba menggambar grafik fungsi kuadrat , , , dan .
Agar gambar grafik semakin bagus, kita perlu menentukan titik yang dilalui grafik sebanyak-banyaknya.

Jika kalian perhatikan perubahan nilai pada keempat tabel di atas, nampak bahwa nilai akan berulang setelah diperoleh . Dengan demikian, titik puncak dari keempat grafik fungsi kuadrat di atas adalah .
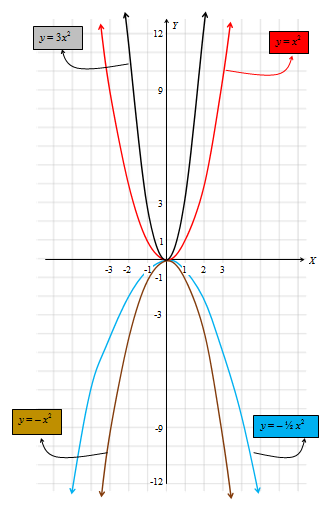
Nah, jika kita hubungkan seluruh titik yang ada pada tabel nilai fungsi di atas pada koordinat Kartesius, maka akan kita peroleh grafik fungsi kuadrat sebagai berikut:

Baca Juga
Jika kalian cermati dengan seksama, ada enam hal yang dapat kita simpulkan, yaitu:
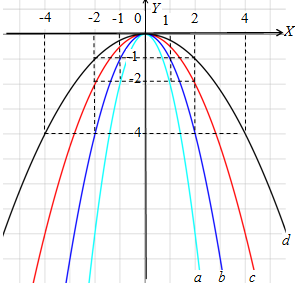
- Jika , maka grafik membuka ke atas.
- Jika maka grafik membuka ke bawah.
- Jika dan semakin besar, maka grafiknya semakin menyempit.
- Jika dan semakin besar, maka grafiknya semakin melebar.
- Grafik simetri terhadap sumbu .
- Titik puncak adalah .
Lalu bagaimanakah sifat grafik fungsi kuadrat berbentuk , dengan dan ?
Yuk kita cermati uraian berikut.
Grafik Fungsi y = ax2 + c
Sebagai ilustrasi, kita akan mencoba menggambar grafik fungsi kuadrat , , , dan .
Denga mensubtitusikan beberapa nilai ke dalam fungsi kuadrat di atas, kita peroleh tabel nilai fungsi sebagai berikut:

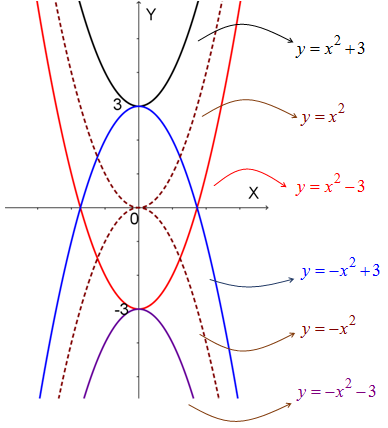
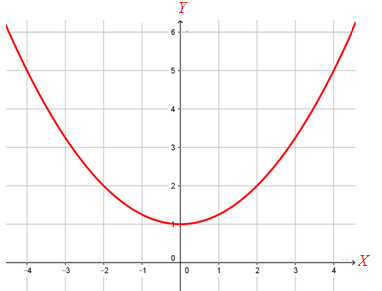
Nah, jika kita hubungkan semua titik pada tabel nilai fungsi di atas dalam koordinat Kartesius, maka akan kita peroleh grafik fungsi kuadrat sebagai berikut:

Coba tebak, apa saja sifat dari grafik fungsi kuadrat berbentuk ?
Jika kita cermati keempat grafik fungsi kuadrat di atas, maka akan kita peroleh hasil sebagai berikut:
- titik puncak grafik fungsi kuadrat adalah
- titik puncak grafik fungsi kuadrat adalah
- titik puncak grafik fungsi kuadrat adalah
- titik puncak grafik fungsi kuadrat adalah
Dengan demikian, dapat kita simpulkan bahwa titik puncak dari grafik fungsi kuadrat , dengan dan adalah .
Tentu sekarang kalian sudah jelas mengenai bagaimana cara menggambar grafik fungsi kuadrat berbentuk dan serta sifat- sifatnya bukan?

S1

Grafik fungsi kuadrat adalah ….
S2

Grafik fungsi kuadrat adalah ….
S3
Grafik fungsi kuadrat melalui titik , , dan . Nilai yang mungkin adalah ….
S4
Grafik fungsi kuadrat adalah ….
S5
Titik-titik berikut dilalui oleh grafik fungsi kuadrat , kecuali …
S6
Jika titik terletak pada grafik fungsi kuadrat , maka nilai adalah …
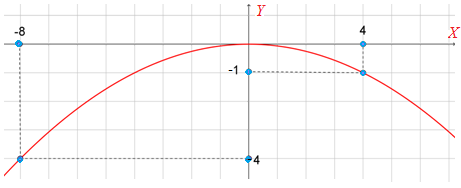
S7

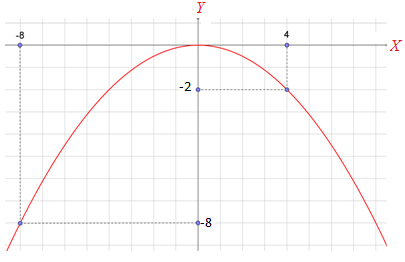
Fungsi kuadrat yang sesuai dengan grafik di atas adalah ....
S8

Fungsi kuadrat yang sesuai dengan grafik fungsi di atas adalah ….
S9
Diketahui grafik fungsi kuadrat melalui titik . Grafik fungsi kuadrat adalah ….
S10

Jika fungsi kuadrat dari grafik di atas adalah , maka grafik fungsi adalah ....
Tags:
matematika







