Contoh Soal Teorema Limit
Contoh Soal Teorema Limit - Pada topik sebelumnya telah didefinisikan mengenai konsep limit fungsi. Definisi tersebut sebagai berikut.
Sementara untuk menyelidiki ada atau tidaknya limit fungsi di suatu titik, kamu telah diajarkan untuk menggunakan teorema limit kiri-limit kanan berikut ini.
Teorema ini dapat pula digunakan untuk menentukan nilai limit fungsinya. Akan tetapi, penggunaan teorema limit kiri-limit kanan untuk menentukan nilai limit fungsi kurang efektif. Untuk itu, kamu dapat menggunakan teorema limit utama yang akan dijelaskan pada topik kali ini.
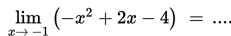
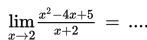
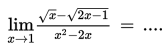
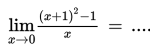
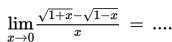
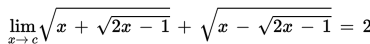
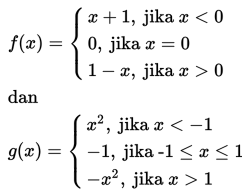
Jika x dekat tetapi tidak sama dengan c mengakibatkan f (x) dekat ke L maka .
Sementara untuk menyelidiki ada atau tidaknya limit fungsi di suatu titik, kamu telah diajarkan untuk menggunakan teorema limit kiri-limit kanan berikut ini.
Teorema Limit Kiri-Limit Kanan
Misalkan fungsi f (x) didefinisikan di sekitar x = c, maka jika dan hanya jika . biasa disebut limit kiri dan biasa disebut limit kanan.
Teorema ini dapat pula digunakan untuk menentukan nilai limit fungsinya. Akan tetapi, penggunaan teorema limit kiri-limit kanan untuk menentukan nilai limit fungsi kurang efektif. Untuk itu, kamu dapat menggunakan teorema limit utama yang akan dijelaskan pada topik kali ini.
Teorema Limit Utama
Misalkan n bilangan asli, k konstanta, serta f dan g fungsi-fungsi yang mempunyai limit di c, maka:
Teorema 1 (T.1) :
Nilai limit suatu fungsi konstan sama dengan konstanta itu.
Teorema 2 (T.2) :
Nilai limit suatu fungsi identitas sama dengan nilai pendekatan peubahnya.
Teorema 3 (T.3) :
Limit hasil kali konstanta dengan fungsi sama dengan hasil kali konstanta dengan limit fungsi itu.
Teorema 4 (T.4) :
Limit jumlah fungsi-fungsi sama dengan jumlah masing-masing limit fungsi.
Teorema 5 (T.5) :
Limit selisih fungsi-fungsi sama dengan selisih masing-masing limit fungsi.
Teorema 6 (T.6) :
Limit hasil kali fungsi-fungsi sama dengan hasil kali masing-masing limit fungsi.
Teorema 7 (T.7) : , syaratnya g (x) ≠ 0
Limit hasil bagi fungsi-fungsi sama dengan hasil bagi masing-masing limit fungsi dengan syarat limit penyebut tidak sama dengan nol.
Teorema 8 (T.8) :
Limit fungsi pangkat n sama dengan pangkat n dari limit fungsi itu.
Teorema 9 (T.9) :
Limit akar pangkat n dari suatu fungsi sama dengan akar pangkat n dari limit fungsi itu dengan syarat limit fungsi tersebut tidak negatif untuk n bilangan genap.
SOAL 1
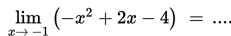
SOAL 2
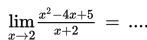
SOAL 3
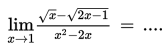
SOAL 4
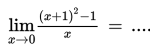
SOAL 5
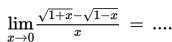
SOAL 6
Nilai c riil yang memenuhi
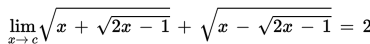
adalah ....
SOAL 7
Jika diketahui
maka = ....
SOAL 8
Jika diketahui f (x) = x2 + 3x
maka
adalah ....
SOAL 9
Jika diketahui
maka = ....
SOAL 10
Diketahui:
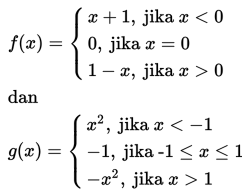
Tags:
MIA kelas 11


