Contoh Soal Peluang Kejadian Saling Bebas
Contoh Soal Peluang Kejadian Saling Bebas - Jika banyak titik sampel pada kejadian K dinyatakan sebagai n (K) dan banyak anggota ruang sampel kejadian K dinyatakan n (S), maka peluang kejadian K dapat dinyatakan dengan:

Mari pahami ilustrasi berikut.
Sebuah dadu dilempar sebanyak 2 kali. Bagaimana menentukan peluang muncul mata dadu 5 pada pelemparan pertama dan muncul mata dadu 2 pada pelemparan kedua?
Penyelesaian:
Misalkan:
A = kejadian muncul mata dadu 5 pada pelemparan pertama
A = kejadian muncul mata dadu 5 pada pelemparan pertama
B = kejadian muncul mata 2 pada pelemparan kedua
Peluang munculnya mata dadu pada pelemparan pertama tidak berpengaruh terhadap peluang munculnya mata dadu pada pelemparan kedua, sehingga A dan B adalah kejadian saling bebas.
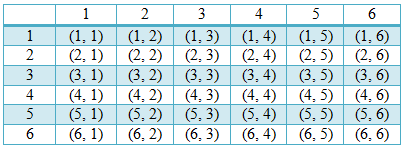
Ruang sampel kejadian mencangkup seluruh kemungkinan mata dadu yang muncul pada pelemparan pertama dan kedua (seperti pada tabel di bawah ini), sehingga n (S) = 36.

A = {(5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6)}
n (A) = 6
n (A) = 6
Baca Juga
- Contoh Soal Konsep limit dalam konteks nyata
- Contoh Soal Menggunakan Fungsi Distribusi Binomial
- Contoh Soal Nilai fungsi dan nilai akar-akar persamaan aljabar
- Contoh Soal Masalah nyata yang berkaitan dengan turunan fungsi trigonometri
- Contoh Soal Penerapan turunan fungsi trigonometri untuk menentukan titik Stasioner
B = {(1, 2), (2, 2), (3, 2), (4, 2), (5, 2), (6, 2)}
n (B) = 6
n (B) = 6
A ∩ B = {(5, 2)}
n (A ∩ B) = 1
n (A ∩ B) = 1
Perhatikan hubungan P (A ∩ B), P (A), dan P (B).
merupakan nilai dari:
P (A ∩ B) = P (A) × P (B)
Hasil di atas menunjukkan bahwa peluang irisan dari dua kejadian yang saling bebas sama dengan hasil kali peluang kedua kejadian tersebut. Hal ini berlaku umum untuk semua kejadian saling bebas, sehingga diperoleh kesimpulan sebagai berikut.
Definisi Kejadian Saling Bebas
Dua kejadian disebut kejadian saling bebas jika kejadian pertama tidak mempengaruhi peluang terjadinya kejadian selanjutnya.
Jika A dan B adalah kejadian saling bebas, maka berlaku:

SOAL 1
Berikut ini yang bukan merupakan kejadian saling bebas adalah ....
SOAL 2
Diketahui P (A) = 0,35 dan P (B) = 0,67. Jika A dan B adalah kejadian saling bebas, maka P (A ∩ B) = ....
SOAL 3
Pada pelemparan sebuah koin sebanyak 2 kali, peluang munculnya sisi gambar pada pelemparan pertama dan muncul sisi angka pada pelemparan kedua adalah ....
SOAL 4
Jika diketahui . Jika E dan F saling bebas satu sama lain, nilai = ....
SOAL 5
Terdapat 2 kotak berisi lampu. Pada kotak pertama terdapat 12 lampu dengan 4 diantaranya rusak. Pada kotak kedua terdapat 15 lampu dengan 3 diantaranya rusak. Peluang terambilnya sebuah lampu rusak masing-masing dari kotak pertama dan kedua adalah ....
SOAL 6
Diketahui W = {A, B, E, I, K, M, T} dan V = {1, 2, 3, 4, 5, 6, 7, 8, 9}. Peluang terpilih satu huruf vokal dari himpunan W dan terpilih satu bilangan kelipatan 3 dari himpunan V adalah ...
SOAL 7
Pada pelemparan sebuah koin dan sebuah dadu secara bersamaan, peluang muncul sisi angka pada koin dan mata dadu bilangan genap adalah ....
SOAL 8
Diketahui kejadian J, K, dan L saling bebas. Jika P (J) = 2P (K) dan , maka peluang kejadian L adalah ....
SOAL 9
Pada sebuah permainan lempar koin, Andi menebak akan muncul sisi gambar sedangkan Banu menebak akan muncul sisi angka. Peluang Andi selalu kalah hingga pelemparan keempat dan menang pada pelemparan kelima adalah ....
SOAL 10
Suatu sekolah memiliki 3 kelas XI IPA yaitu kelas A, B, dan C. Di kelas A terdapat 15 siswa dan 17 siswi. Di kelas B terdapat 16 siswa dan 14 siswi. Di kelas C terdapat 11 siswa dan 22 siswi. Jika dari masing-masing kelas akan dipilih 1 orang perwakilan, maka peluang terpilih siswa dari kelas A dan B, serta siswi dari kelas C adalah ....
Tags:
MIA kelas 11







