Contoh Soal Gelombang Stasioner
Contoh Soal Gelombang Stasioner - Gelombang stasioner terbentuk dari superposisi/ perpaduan gelombang datang dan gelombang pantul. Tali dapat membentuk gelombang stasioner jika salah satu ujungnya diikatkan pada suatu tiang. Apabila salah satu ujung tali digerakkan dan gelombangnya sampai di ujung lain yang terikat, maka gelombang tersebut akan terpantul kembali ke posisi awalnya. Jika hal itu berlangsung secara terus menerus, akan terbentuk gelombang stasioner atau gelombang berdiri (standing wave). Berdasarkan keadaan ujung talinya, gelombang stasioner dibedakan menjadi dua, yaitu ujung tetap dan ujung bebas.
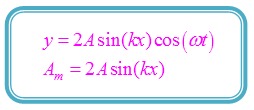


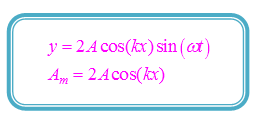



🌈 Gelombang Stasioner Ujung Tetap
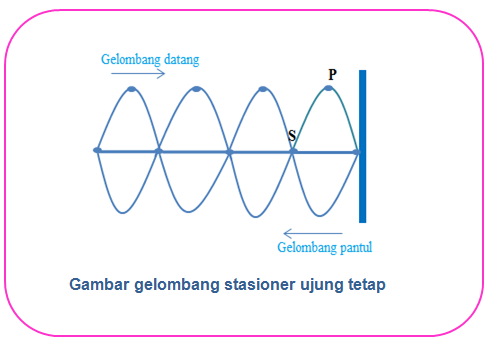
Gelombang stasioner ujung tetap terjadi ketika salah satu ujung tali terikat kuat pada tiang, sehingga ujung tersebut tidak dapat bergerak. Saat tali digetarkan, akan ada gelombang yang merambat dari ujung tali yang bebas menuju tiang/ ujung tetap. Gelombang yang merambat ini dinamakan gelombang datang. Saat mengenai ujung tetap, gelombang ini akan dipantulkan sehingga terjadi interferensi gelombang. Gelombang hasil pantulan ini disebut sebagai gelombang pantul.

Misalkan gelombang datang dinyatakan sebagai berikut:
Dengan demikian, gelombang pantul yang terbentuk adalah gelombang yang sama dengan fase yang berlawanan, yaitu:
Oleh karena -sin α = sin (-α), maka:
Jika kedua gelombang mengalami perpaduan atau superposisi, maka gelombang total dirumuskan sebagai berikut.
Oleh karena sin α + sin β = 2 sin (α + β) cos (α - β), maka persamaan di atas dapat disederhanakan sebagai berikut.
Dengan demikian, simpangan dan amplitudo gelombang stasioner ujung tetap dapat dituliskan sebagai berikut.
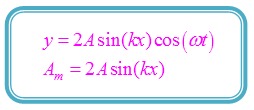
Keterangan:
y = simpangan gelombang stasioner ujung tetap (m);
A = amplitudo gelombang berjalan; dan
Am = 2A sin (kx) = amplitudo superposisi (m).
Berdasarkan persamaan di atas, Am dapat bernilai minimum dan maksimum. Kapan Am bernilai maksimum dan minimum?
⓵ Am akan bernilai maksimum jika sin (kx) = ± 1. Kondisi tersebut akan terpenuhi pada x berikut.

Posisi Am maksimum tersebut biasa dikenal sebagai letak perut.
⓶ Am akan bernilai minimum jika sin (kx) = 0. Keadaan tersebut akan terpenuhi pada x berikut.

Posisi Am minimum tersebut biasa dikenal sebagai letak simpul.
🌈 Gelombang Stasioner Ujung Bebas
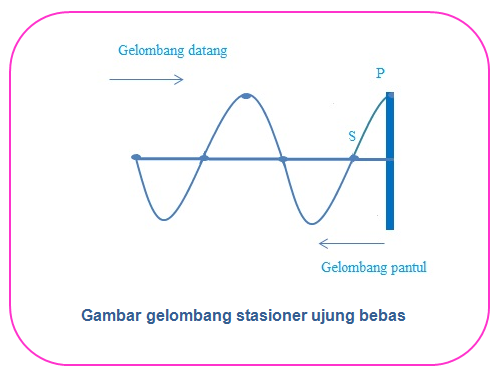
Gelombang stasioner ujung bebas terjadi saat salah satu ujung tali terikat longgar pada tiang, sehingga ujung tersebut bebas bergerak naik dan turun.

Misalkan gelombang datang dinyatakan sebagai berikut:
Dengan demikian, gelombang pantul yang terbentuk adalah gelombang yang sama dengan fase yang sama pula, yaitu:
Oleh karena -sin α = sin (-α), maka:
Jika kedua gelombang mengalami perpaduan atau superposisi, maka gelombang total dirumuskan sebagai berikut.
Oleh karena sin α - sin β = 2 cos (α + β) sin (α - β), maka persamaan di atas dapat disederhanakan sebagai berikut.
Dengan demikian, simpangan dan amplitudo gelombang stasioner ujung bebas dapat dituliskan sebagai berikut.
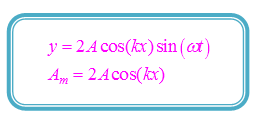
Keterangan:
y = simpangan gelombang stasioner ujung bebas (m);
A = amplitudo gelombang berjalan; dan
Am = 2A cos (kx) = amplitudo superposisi (m).
Berdasarkan persamaan di atas, Am dapat bernilai minimum dan maksimum. Kapan Am bernilai maksimum dan minimum?
⓵ Am akan bernilai maksimum jika cos (kx) = ±1. Kondisi tersebut akan terpenuhi pada x berikut.

Posisi Am maksimum tersebut biasa dikenal sebagai letak perut.
⓶ Am akan bernilai minimum jika cos (kx) = 0. Keadaan tersebut akan terpenuhi pada x berikut.

Posisi Am maksimum tersebut biasa dikenal sebagai letak simpul.
Nah, lebih kompleks kan persamaan pada gelombang stasioner? Agar kalian lebih mudah membedakannya, perhatikan tabel berikut ini.

SOAL 1
Gelombang yang memiliki nilai amplitudo berbeda-beda di setiap titik disebut ….
SOAL 2
Gelombang pantul yang bentuk gelombangnya sama dengan gelombang datang, tetapi fasenya berlawanan terjadi pada ….
SOAL 3
Suatu gelombang bergerak dengan persamaan berikut.
Beradasarkan persamaan di atas, jenis gelombangnya adalah ….
SOAL 4
Jarak antara simpul dan perut yang berdekatan pada gelombang stasioner adalah 20 cm. Jika cepat rambat gelombangnya 300 m/s, maka frekuensi gelombang tersebut adalah ….
SOAL 5
Suatu gelombang stasioner bergerak dengan persamaan berikut.
Jika posisi interferensi gelombang berada pada x = 0,5 m, maka amplitudo superposisinya adalah ….
SOAL 6
Jika simpul ke-5 suatu gelombang stasioner ujung bebas berada pada x = 22 cm, maka panjang gelombangnya adalah ….
SOAL 7
Gelombang tali yang ujungnya terikat memiliki persamaan berikut.
Jika x, y dalam m dan t dalam sekon, maka jarak antara dua simpul yang berdekatan adalah ….
SOAL 8
Gelombang stasioner ujung tetap bergerak dengan frekuensi 3 Hz. Jika jarak antara dua perut yang berdekatan adalah 1 m, maka cepat rambat gelombangnya adalah ….
SOAL 9
Perhatikan persamaan gelombang stasioner berikut.
Jika amplitudo superposisinya 5 m, maka nilai x adalah ….
SOAL 10
Suatu tali yang ujungnya terikat tetap memiliki persamaan gelombang datang dan pantul sebagai berikut.
1. Persamaan gelombang datang
2. Persamaan gelombang pantul
Persamaan gelombang setelah mengalami superposisi adalah ….
Tags:
Contoh Soal Fisika


